甘肃省张掖市2016届高三下学期第三次诊断考试数学(理)试题及答案
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数
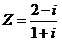
的共轭复数对应的点在复平面内位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.若α∈R,则“α=0”是“sin α《cos α”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.设
为等差数列

项和,若
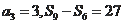
,则该数列的首项
等于( )
A.
B.
C.
D.
4. 某程序的框图如图所示,执行该程序,若输入的N =5,则输出i =( )
A.6 B.7 C.8 D.9
5.双曲线
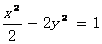
的渐近线与圆
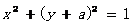
相切,则正实数a的值为 ( )
A.
B.
C.
D.
 #p#分页标题#e#
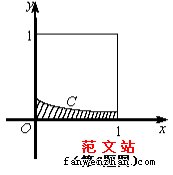
#p#分页标题#e#6.在如图所示的正方形中随机投掷10 000 个点,
则落入阴影部分(曲线C 为正态分布N(-1,1)
的密度曲线)的点的个数的估计值为( )
A.1 193 B.1 359 C.2 718 D.3 413
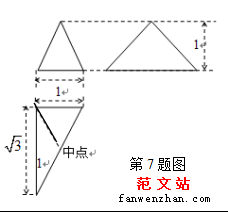
7.已知三棱锥的三视图如图所示,则它的外接球表面积为( )
A.16
B.4
C.8
D.2
8.已知
,函数
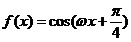
在
上单调递增,则
的取值范围是( )
A.
B.
C.
D.
9.在
中,
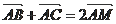
,
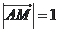
,点
在
上且满足
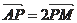
,则
#p#分页标题#e#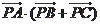
等于( )
A.
B.
C.
D.
10.已知二次函数
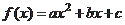
的导数
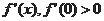
,且
的值域为
,则
的最小值为( ) A.3 B.
C.2 D.
11.已知椭圆
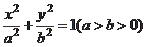
的左、右焦点分别为
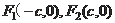
,若椭圆上存在点P使

,则该椭圆的离心率的取值范围为( )
A.(0,
B.(
) C.(0,
) D.(
,1)
12.已知函数
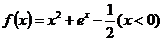
与
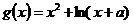
图象上存在关于
轴对称的点,则
的取值范围是( )
A.
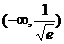
B.
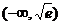
C.
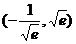
D.
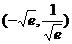
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分.
13.二项式

的展开式中常数项为 .
14.若变量x,y满足约束条件

且z=5y-x的最大值为a,最小值为b,则a-b的值是 。
15.我们知道,在边长为
的正三角形内任一点到三边的距离之和为定值
,类比上述结论,在棱长为
的正四面体内任一点到其四个面的距离之和为定值,此定值为 。
16.设数列


满足
=2,
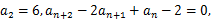
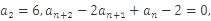
若表示不超过x的最大整数,则

==
三、解答题:本大题共6小题, 共70分, 解答时应写出必要的文字说明、证明过程或演算步骤。
17.(本小题满分12分)
设函数
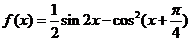
.
(Ⅰ)若
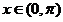
,求
的单调递增区间;
(Ⅱ)在锐角
中,角
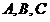
的对边分别为
,若
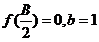
,求
面积的最大值.
18.(本小题满分12分)
某超市从2016年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,并按,(10,20],(20,30],(30,40],(40,50]分组,得到频率分布直方图如下:
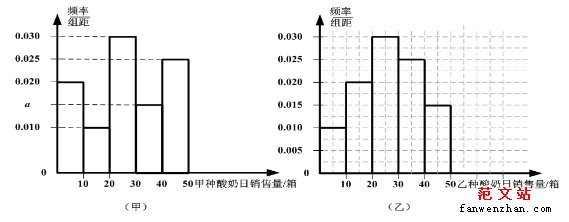
假设甲、乙两种酸奶独立销售且日销售量相互独立.
(Ⅰ)写出频率分布直方图(甲)中的
的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为
,
,试比较
与
的大小;(只需写出结论);
(Ⅱ)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率;
(Ⅲ)设
表示在未来3天内甲种酸奶的日销售量不高于20箱的天数,以日销售量落入各组的频率作为概率,求
的数学期望.
19.(本小题满分12分)
在直三棱柱
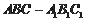
中,
,∠ACB=90°,M是
的中点,N是
的中点。
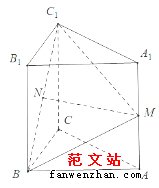
(Ⅰ)求证:MN∥平面
;
(Ⅱ)求点
到平面BMC的距离;
(Ⅲ)求二面角
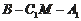
的平面角的余弦值大小。
20.(本小题满分12分)
设抛物线C的方程为x2 =4y,M为直线l:y=-m(m》0)上任意一点,过点M作抛物线C的两条切线MA,MB,切点分别为A,B.
(Ⅰ)当M的坐标为(0,-l)时,求过M,A,B三点的圆的标准方程,并判断直线l与此圆的位置关系;
(Ⅱ)当m变化时,试探究直线l上是否存在点M,使MA ⊥MB?若存在,有几个这样的点,若不存在,请说明理由。
21.(本小题满分12分)
设函数
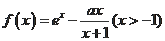
.
(Ⅰ)当
时,讨论
#p#分页标题#e#
的单调性;
(Ⅱ)当
时,设
在
处取得最小值,求证:
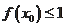
.
22.。选修4-1:几何证明选讲(本小题满分10分)
如图,
是圆
的直径,
是弦,
的平分线
交圆
于点
,
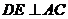
,交
的延长线于点
,
交
于点
.
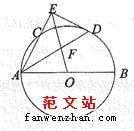
(Ⅰ)求证:
是圆
的切线;
(Ⅱ)若
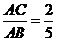
,求
的值.
23.选修4-4:坐标系与参数方程(本小题满分10分)
选做题:在直角坐标系
中,曲线
的参数方程为
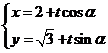
(
是参数),以原点
为极点,
轴正半轴为极轴建立极坐标系,曲线
的极坐标方程为
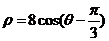
.
(Ⅰ)求曲线
的直角坐标方程,并指出其表示何种曲线;
(Ⅱ)若曲线
与曲线
交于
,
两点,求
的最大值和最小值.
24.选修4—5:不等式选讲(本小题满分10分)
已知函数

,
,且
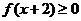
的解集为
.
(Ⅰ) 求
的值;
(Ⅱ) 设a,b,c为正数,且a+b+4c=m没,求++的最大值.
高三数学(理科)答案
一、选择题(本大题共12题,每小题5分,共60分)
题号123456789101112
答案AADACBBDDCDB
11.【解析】根据正弦定理得
,所以由

可得
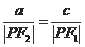
,即
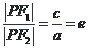
,所以

,又
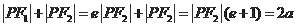
,即
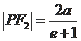
,因为
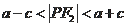
,(不等式两边不能取等号,否则分式中的分母为0,无意义)所以
 #p#分页标题#e#
#p#分页标题#e#,即
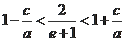
,所以

,即

,所以
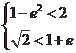
,解得

,即
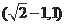
,选D.
12 B
法一由题意存在
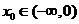
满足
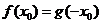
得
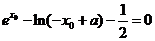
令
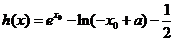
因为
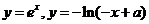
在定义域内都是单调递增的
所以

在定义域内都是单调递增的,
又因为x趋近于
时函数h(x)《0且

在
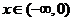
上有解
当
时,当
趋近于
时,

趋近于
,所以符合题意。
当
时,
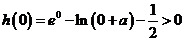

,
综上
,故选B.
【考点定位】指对数函数 方程 单调性
法二由题意存在

满足
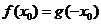
得

即
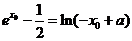
,分别作出
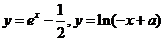
的图像,利于图像数形结合可得
二、填空题:(本大题共4小题,每小题5分,共20分)
13. 7 ; 14. 24 ; 15.
; 16. 2015.
三、解答题:解答应写出文字说明,证明过程或演算步骤(共6题,共70分)
17.(第1问6分,第2问6分)
解:(1)由题意可知,
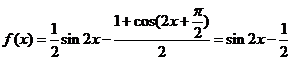
,

由余弦定理
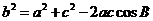 #p#分页标题#e#
#p#分页标题#e#,可得:
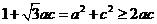
,即
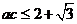
,且当
时等号成立,因此
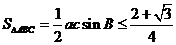
,所以
面积的最大值为
.
18解:(Ⅰ)
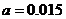
; ………………2分
。 ………………4分
(Ⅱ)设事件
:在未来的某一天里,甲种酸奶的销售量不高于20箱;
事件
:在未来的某一天里,乙种酸奶的销售量不高于20箱;
事件
:在未来的某一天里,甲、乙两种酸奶的销售量恰好一个高于20箱且另一个不高于20箱。 则
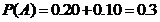
,
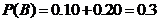
。 …………6分
所以
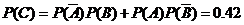
。 …………8分
(Ⅲ)由题意可知,
的可能取值为0,1,2,3. …………9分#p#分页标题#e#
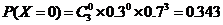
,
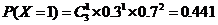
,
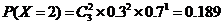
,

。
所以
的分布列为
0123
0.3430.4410.1890.027
…11分
所以
的数学期望

。
……12分
另解:由题意可知
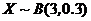
。
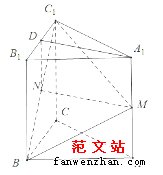
所以
的数学期望
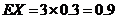
。
19.【答案】(Ⅰ)如图所示,取B1C1中点D,连结ND、A1D
∴DN∥BB1∥AA1
又DN=

∴四边形A1MND为平行四边形。
∴MN∥A1 D 又 MN
平面A1B1C1 AD1
平面A1B1C1
∴MN∥平面#p#分页标题#e#
--------------------4分
(Ⅱ)因三棱柱

为直三棱柱, ∴C1 C ⊥BC,又∠ACB=90°∴BC⊥平面A1MC1
在平面ACC1 A1中,过C1作C1H⊥CM,又BC⊥C1H,故C1H为C1点到平面BMC的距离。在等腰三角形CMC1中,C1 C=2
,CM=C1M=
∴
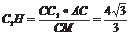
。--------------------------8分
(Ⅲ)在平面ACC1A1上作CE⊥C1M交C1M于点E,A1C1于点F,
则CE为BE在平面ACC1A1上的射影,
∴BE⊥C1M, ∴∠BEF为二面角B-C1M-A的平面角,
在等腰三角形CMC1中,CE=C1H=
,∴tan∠BEC=
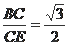
∴ cos∠BEC=
。
二面角

的平面角与∠BEC互补,所以二面角
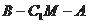
的余弦值为
--------------------12分
法2:(Ⅰ)同上。如图所示建系,
(Ⅱ)可得,
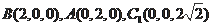
,
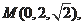
,设

是平面BMC的法向量,C1点到平面BMC的距离h。#p#分页标题#e#
可求得一个法向量为
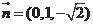
,
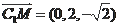
,
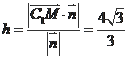
(Ⅲ)可知

是平面
的法向量,设

是
平面
的法向量,求得一个法向量
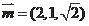
设
是为二面角
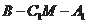
的平面角,则
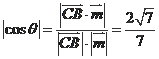
,又因为二面角
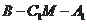
的平面角是钝角,所以
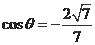
。
20.【答案】解:(Ⅰ)当M的坐标为
时,
设过M点的切线方程为
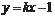
,代入
,整理得
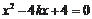
,①
令
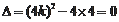
,解得
,
代入方程①得
,故得
,

。
因为M到AB的中点(0,1)的距离为2,
从而过
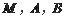
三点的圆的标准方程为
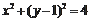
.
易知此圆与直线l:y=-1相切。 ………………………………………………………(6分)
(Ⅱ)设切点分别为

、
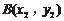
,直线l上的点为M
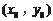
,
过抛物线上点
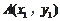
的切线方程为
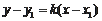
,因为

,
,
从而过抛物线上点

的切线方程为
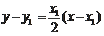 #p#分页标题#e#
#p#分页标题#e#,又切线过点
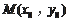
,
所以得

,即
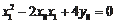
。
同理可得过点

的切线方程为
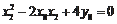
,………………………(8分)
因为
,
且
是方程
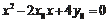
的两实根,
从而,
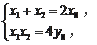
所以
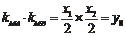
,
当
,即
时,
直线
上任意一点M均有MA⊥MB,…………………………………………………(10分)
当
,即m≠1时,MA与MB不垂直。
综上所述,当m =1时,直线
上存在无穷多个点M,使MA⊥MB,当m≠1时,直线l
上不存在满足条件的点M.……………………………………………………………(12分)
21试题解析:(Ⅰ)当
时,
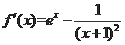
因为
单调递增,
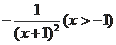
单调递增,所以
在
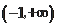
单调递增,
且
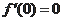
,因此当

时,
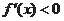
;当
时,

故
在
单调递减,在
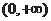
单调递增………………4分
(Ⅱ)当
时,
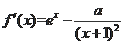 #p#分页标题#e#
#p#分页标题#e#,因为
单调递增,

单调递增,所以
在
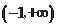
单调递增.又
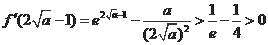
,…6分
当
满足

且
时,
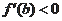
,故
存在唯一零点,设零点为
当
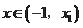
时,
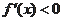
;当
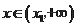
时,

.故
在
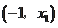
单调递减,在
 #p#分页标题#e#
#p#分页标题#e#单调递增,所以当
时,
取得最小值,由条件可得
,
的最小值为
. ………8分
由于

,所以

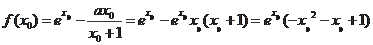
设
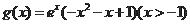
………10分
则
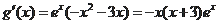
令
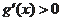
,得
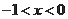
;令
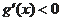
,得
故
在
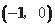
单调递增,
单调递减,
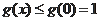
故
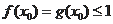
.…………12分
考点:1.含参函数的单调性;2.用导数知识研究函数零点问题.
22【答案】(Ⅰ)见解析;(Ⅱ)
.
【解析】
试题分析:(Ⅰ)连接
,易证得
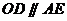
,从而由已知条件垂直关系可证得
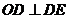
,进而使问题得证;(Ⅱ)过
作

于点
,连接
,求出
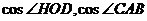
的值,通过
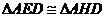
与
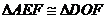
求出比值.
试题解析:(1)连接
,可得
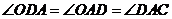
,∴
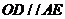
,
又
 #p#分页标题#e#
#p#分页标题#e#,∴

,又
为半径,∴
是圆
的切线.
(Ⅱ)过
作

于点
,连接
,则有
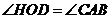
,
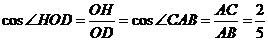
,
设
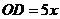
,则
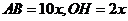
,∴
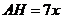
,
由

可得
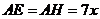
,又由

,可得
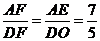
.
考点:1.切线的性质;2、比例线段.
23.【答案】(Ⅰ)曲线
的直角坐标方程为
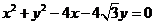
,其表示一个圆;(Ⅱ)最小值为
,最大值为
.
【解析】
试题分析:(Ⅰ)利用

,
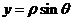
可将
的极坐标方程化为相应直角方程,即可求解;(Ⅱ)联立
,
的方程,将
表示为相应的函数关系式,从而求解.
试题解析:(1)对于曲线
有

,即

,因此曲线
的直角坐标方程为

,其表示一个圆;(2)联立曲线
与曲线
的方程可得:
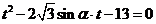
,
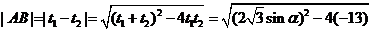

,因此
的最小值为
,最大值为
.
考点:1.极坐标方程与直角坐标方程的相互转化;2.直线与圆的位置关系
24.【答案】(1)
;(2)9.
(1)因为
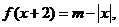
故
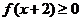
等价于
由
得
,且其解集为

又因
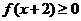
的解集为
,故m=1……………………。.5

(2) 设a,b,c为正数,且a+b+4c=m没,求++的最大值.
解:由(1)得a+b+4c=1
由柯西不等式得(++)2≤22·=25, ∴++≤210. 故++的最大值是210………….5